Lecture 14 Notes

Correlated features

One prior distribution for each cluster

1. One feature: one-dimensional distribution, eg. a varying intercepts (\(\alpha_{j} \sim Normal(\bar{\alpha}, \sigma)\))
2. Two features: two-dimensional distribution, ideally not two 1-D distributions but one 2-D distribution (\([\alpha_{j}, \beta_{j}] \sim MVNormal([\bar{\alpha}, \bar{\beta}], \sum)\))
3. N features: N-dimensional distribution (\([\alpha_{j, 1...N}] \sim MVNormal(A, \sum)\))

Correlated varying effects take priors that learn correlation structure using partial pooling across features.

Model specification

\([\alpha_{j}, \beta_{j}] \sim MVNormal([\bar{\alpha}, \bar{\beta}], R, [\sigma, \tau])\)

• \([\alpha_{j}, \beta_{j}]\): features for district j
• \(MVNormal\)
  • \([\bar{\alpha}, \bar{\beta}]\): feature means
  • \(R\): correlation matrix
  • \([\sigma, \tau])\): standard deviations

\(R \sim LKJCorr(4)\)

The LKJ prior is a prior distribution for correlations

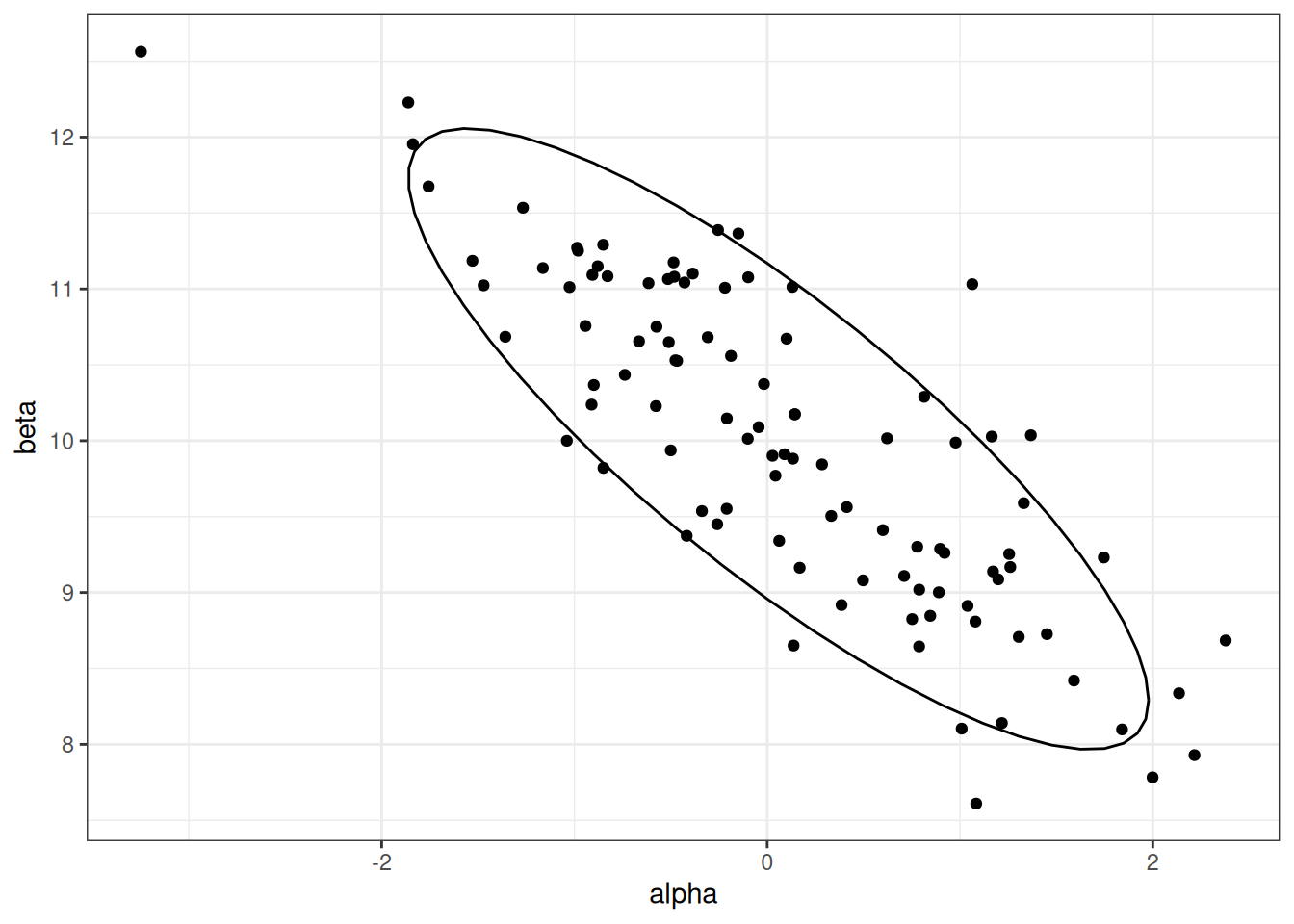
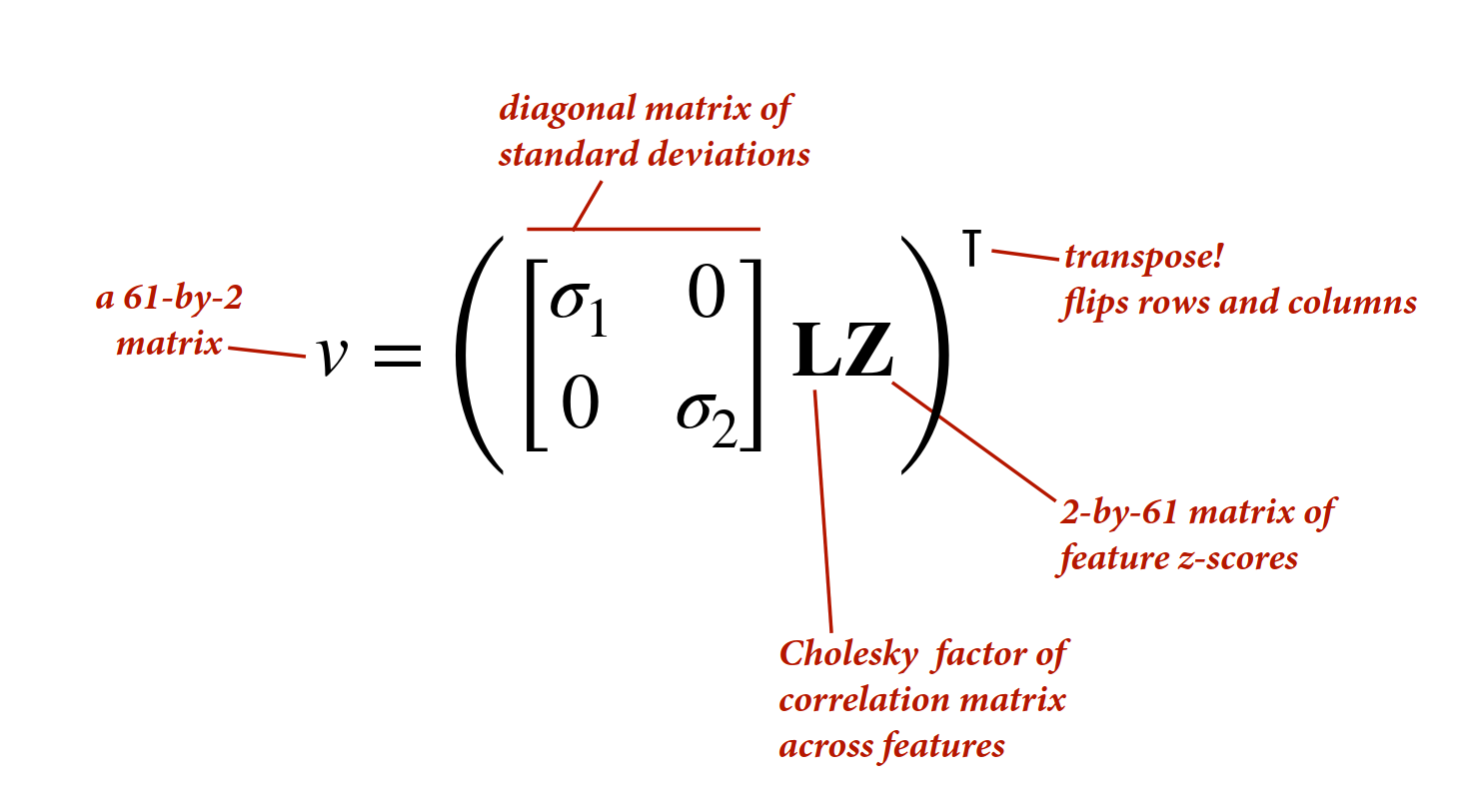
alpha_bar <- 0
beta_bar <- 10
mu <- c(alpha_bar, beta_bar)

rho <- -0.8
R <- matrix(c(1, rho, rho, 1), 2, 2)

n <- 100
mvnorm_prior <- rmvnorm(n, mu, sigma = R)

ggplot(data.frame(mvnorm_prior), aes(X1, X2)) + 
    geom_point() + 
    stat_ellipse(level = .89) + 
    labs(x = 'alpha', y = 'beta') + 
    theme_bw()

Example: Bangladesh fertility survey

Outcome: contraceptive use

Variables: age, living children, urban/rural, districts

coords <- data.frame(
    name = c('A', 'C', 'D', 'K', 'U'),
    x =    c(1,    2,    3,   1.5, 2.5),
    y =    c(0,    0.5,    0,  -1, -1)
)
dagify(
    C ~ A + K + D + U,
    K ~ A + U,
    U ~ D,
  coords = coords
) |> ggdag(seed = 2, layout = 'auto') + theme_dag()

From the previous lecture, the varying intercepts for district and slopes for urban.

\(C_{i} \sim Bernoulli(D_{i}, p_{i})\)

\(logit(p_{i}) = \alpha_{D[i]} + \beta_{D[i]}U_{i}\)

\(\alpha_{j} = \bar{\alpha} + Z_{\alpha, j} * \sigma\)

\(\beta_{j} = \bar{\beta} + Z_{\beta, j} * \sigma\)

\(Z_{\alpha, j} \sim Normal(0, 1)\)

\(Z_{\beta, j} \sim Normal(0, 1)\)

\(\bar{\alpha}, \bar{\beta} \sim Normal(0, 1)\)

\(\sigma, \tau \sim Exponential(1)\)

There is useful information to transfer across features, here we note there is a correlation between rural and urban probability of use within districts. A model that uses two 1-dimensional distributions (intercepts and slopes) does not consider the covariance structure between rural and urban within district.

Comparing the centered and non-centered model specification for the model using the multivariate normal specification with correlated features.

Simulating synthetic data for this kind of complex system is challenging and is likely best done with more detailed tools than eg. expecting a linear responses, instead with eg. an agent based model.

Divergent transitions

Because of high curvature, the physics simulation runs off the surface. One option is to choose a smaller step size, but this results in much longer sampling time. Alternatively, re-express the “centered” model as a “non-centered” model.