Lecture 12 Notes

Multilevel models

Repeat observations within groups can be modeled using categorical variables eg. a vector of alphas for each individual. Categorical variables have anterograde amnesia, when estimating eg. the beta for an individual, this estimate does not contribute anything to the next individual.

Multilevel models are made up of two kinds of models

1. Model observations of groups/individuals
2. Model populations of groups/individuals (clusters)

The population model creates a kind of memory. Advantages of multilevel model include:

• more efficient estimation
• resists overfitting

The order that we estimate clusters does not matter, because we update the population level model with every cluster estimate and that population level model contributes to all clusters’ estimates. The information gathered from each cluster is pooled.

Regularization

Types of pooling:

• Complete pooling where all clusters are the same. This results in underfitting because the model is not complex enough for the variation in the sample.
• No pooling where all clusters are unrelated. This results in overfitting because there may be only a small amount of data for any particular individual/group .
• Partial pooling, an adaptive compromise. There is shrinkage towards the global mean.

Regularization with multilevel models is partial pooling, an adaptive compromise.

Example: cafes

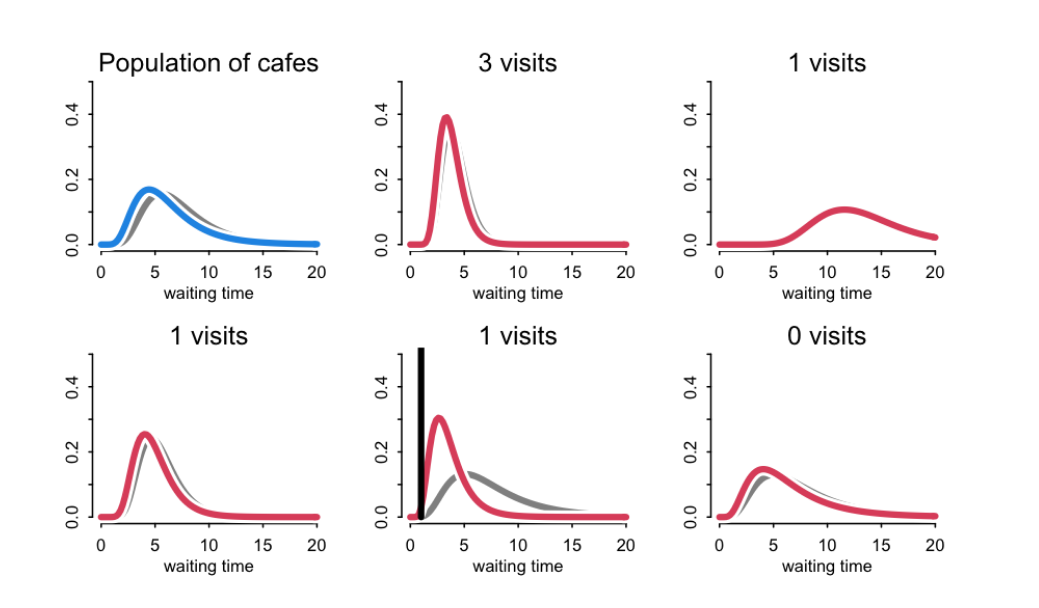
Top left plot is the population of cafes and the remaining plots are individual cafes. The black line is the current observation. The grey distribution is the previous posterior distributions, now prior distributions. The prior of an unobserved cafe is similar to previously observed cafes. The posterior distribution of all other cafes are updated when you observe a new cafe or an old cafe again. The population model learns variation from all cafes.

Reminder: the minimum sample size is 1

Example: reedfrogs

• 48 tanks (T) of reedfrogs
• treatments: density (D), size (G), predation (P)
• outcome: survival (S)

coords <- data.frame(
    name = c('D', 'G', 'P', 'T', 'S'),
    x =    c(1,    2,   3,   1,    2),
    y =    c(0,    0,   0,   1,  1)
)

dagify(
    S ~ D + G + P + T,
  coords = coords
) |> ggdag(seed = 2, layout = 'auto') + theme_dag()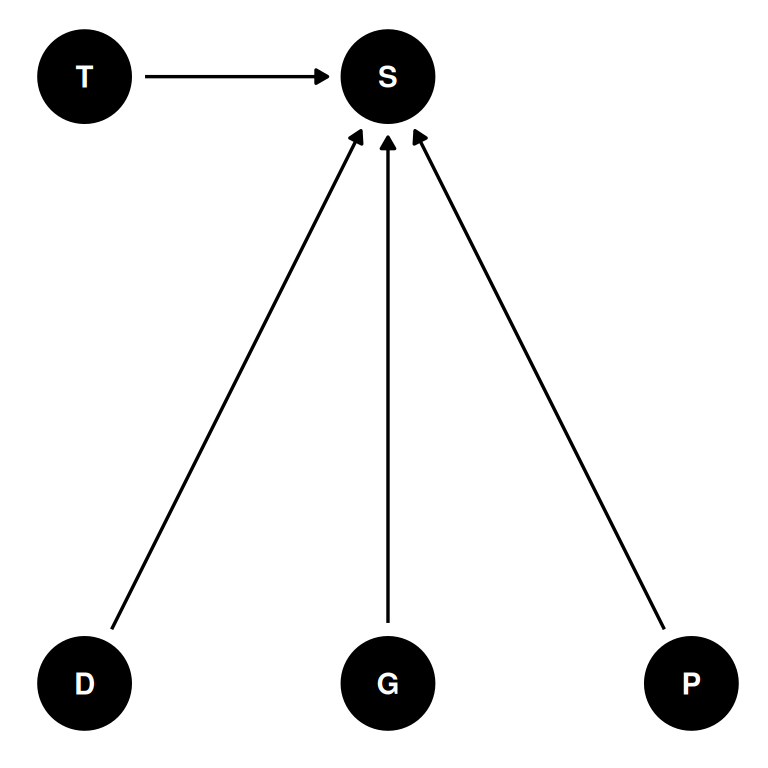

\(S_{i} \sim Binomial(D_{i}, p_{i})\)

\(logit(p_{i}) = \alpha_{T[i]}\)

\(\alpha_{j} \sim Normal(\bar{\alpha}, \sigma)\)

\(\bar{\alpha} \sim Normal(0, 1.5)\)

Alpha bar

Alpha bar represents average alpha that has a Normal(0, 1.5) prior.

Sigma

Sigma corresponds to variability of tanks (alphas).

\(\alpha_{j} \sim Normal(\bar{\alpha}, 0.1)\)

At sigma = 0.1, we tell the model that the tanks are all very similar and the result is estimates for each tank that are all close to the average tank.

\(\alpha_{j} \sim Normal(\bar{\alpha}, 5)\)

At sigma = 5, we tell the model that the tanks vary a lot and the prior does not create any constraints. This is equivalent to a categorical variable with anterograde amnesia where estimates are very close to their values with in-essence no pooling across tanks.

If we manually select a value for sigma, we are choosing the width for the prior distribution for the population and this allows estimates to be more/less different from each other.

There is an optimal sigma for learning between total pooling/underfitting and no pooling/overfitting. We can find the optimal sigma using cross validation and comparing the PSIS values of each model. Note, this is different than defining a prior using the model fit to the sample data because we are evaluating how the model fits to out of sample data (cross validation).

\(\alpha_{j} \sim Normal(\bar{\alpha}, 1.79)\)

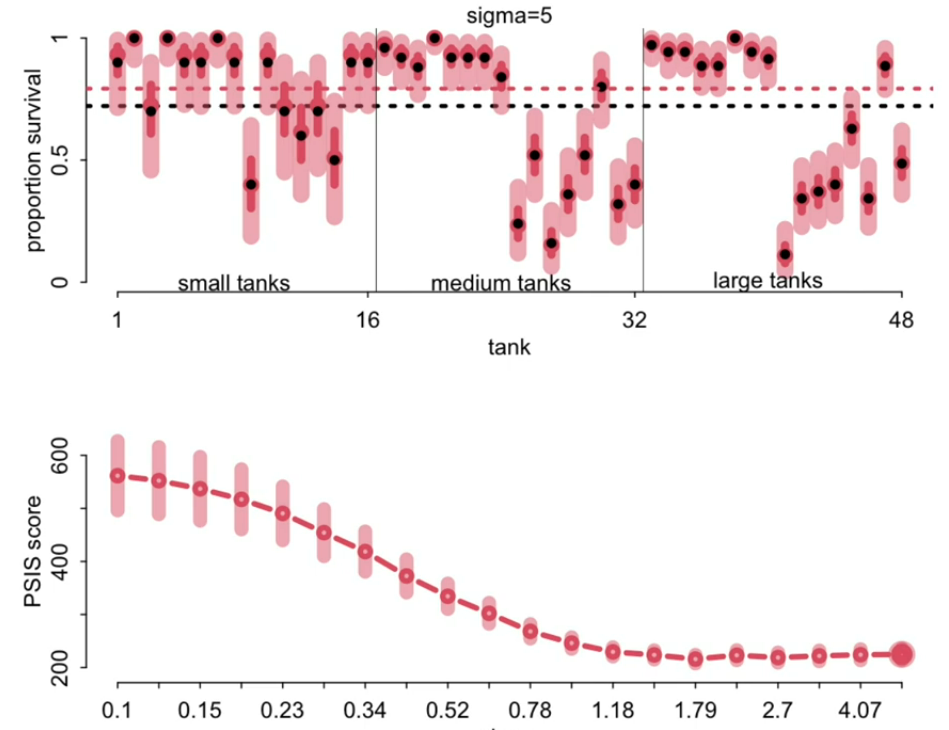
At the optimal sigma determined for this data, the estimate is not exactly at the observed value and we see shrinkage across the tanks towards the global mean.

Alternatively, we can estimate it as a parameter in the model.

\(S_{i} \sim Binomial(D_{i}, p_{i})\)

\(logit(p_{i}) = \alpha_{T[i]}\)

\(\alpha_{j} \sim Normal(\bar{\alpha}, \sigma)\)

\(\bar{\alpha} \sim Normal(0, 1.5)\)

\(\sigma ~ Exponential(1)\)

Alpha j is a mixture of normal distributions with different means and variations.

Estimates

The posterior distribution for sigma is around the range that we expected from the PSIS approach.

Comparing the multilevel model (more parameters) to a model fit with a fixed sigma (less parameters), we see that the multilevel model has a better WAIC estimate which indicates it has less overfitting. This is contrary to the expectation that more parameters leads to more overfitting since multilevel models reduce overfitting.

The estimates for smaller tanks (with less frogs/observations) have smaller evidence and result in more conservative estimates (closer) to the global mean. Alternatively, larger tanks with more observations are less conservative.

Predators

Stratifying by predators absent/present, we see a reduction in tank level survival (obviously). But the interesting thing is that the predictions between the model with and without predators is extremely similar. The difference is, however, in the sigma values where the model with predators has an estimate sigma around half that of the model without predators. The predator variable has explained approximately half of the variation on the log odds scale of the tanks.

To emphasize, sigma is not the variation among the units, it’s the variation among the parameters net all the other effects in the model.

Varying effects

Recommended default is to use partial pooling if there are >1 clusters

Superstitions:

1. Units must be sampled at random
2. Number of units must be large
3. Assumes Gaussian variation

Practical difficulties

1. How to use more than one cluster type at the same time?
2. How to sample efficiently?
3. Slopes? Confounds?

Bonus: random confounds

Random confounds, when unobserved group features influence individually-varying causes. Group-level variables can have direct and indirect influences. Unmeasured features of the group can affect the response directly and indirectly through the traits of individuals.

Related terminology..

• group-level confounding
• endogeneity
• correlated errors
• econometrics

Options:

1. Fixed effects model. Inefficient but soak up group-level confounding. Cannot identify group-level effects.
2. Multilevel model. Better estimates for group-level variables but worse estimates for individual-level effects.
3. Mundlak machine. Estimate a different average rate for each group but not efficient and doesn’t respect the uncertainty in X-bar.

Or use a latent measurement error model.

Example: reedfrogs

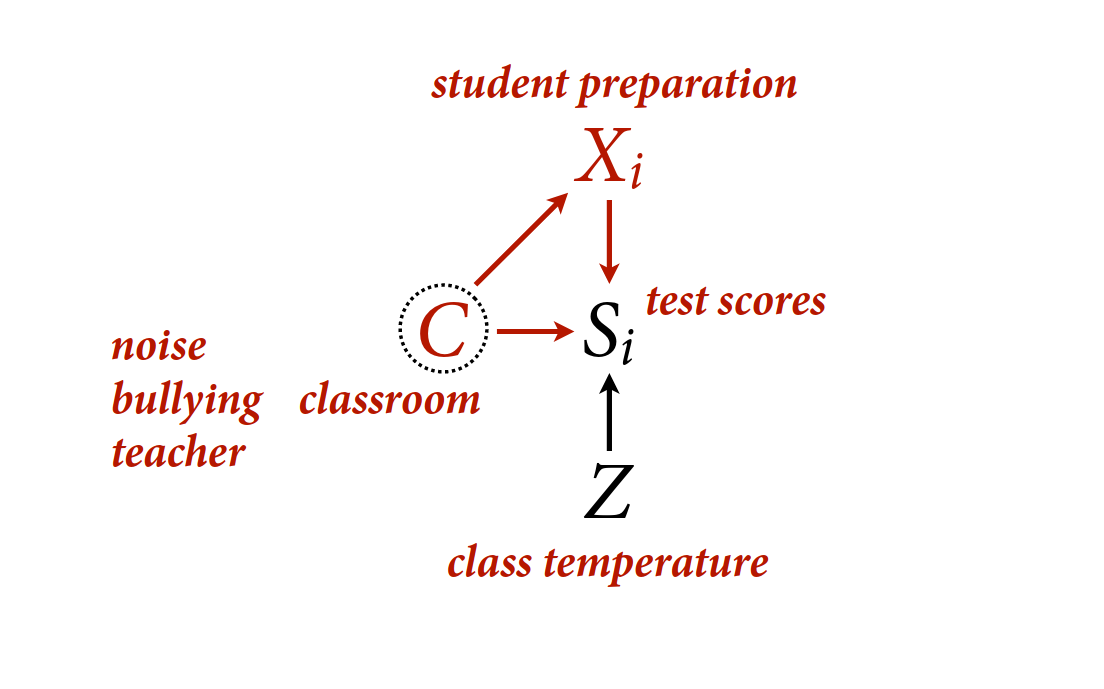
Estimand: \(p(S|do(X))\), the distribution of survival intervening on X.

The problem: there is a backdoor path through G

• Z group level trait
• X individual level trait

coords <- data.frame(
    name = c('G', 'S', 'X', 'Z'),
    x =    c(1,    2,    2,   2),
    y =    c(0,    0,    2,  -1)
)

dagify(
    S ~ G + X + Z,
    X ~ G,
  coords = coords
) |> ggdag(seed = 2, layout = 'auto') + theme_dag()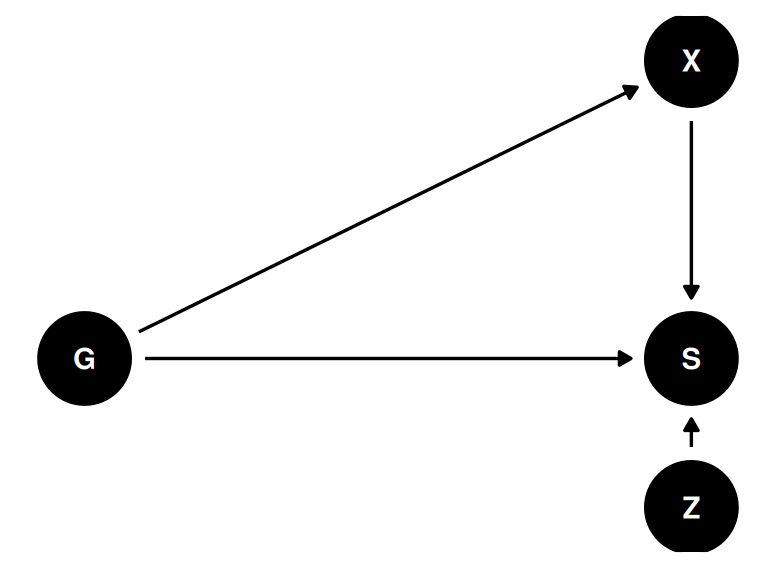

Example: classrooms