dag <- dagify(
S ~ Q + J,
Q ~ X,
J ~ Z,
coords = coords,
exposure = 'Q',
outcome = 'S',
latent = c('Q', 'J')
)
ggdag(dag, seed = 2, layout = 'auto') + theme_dag()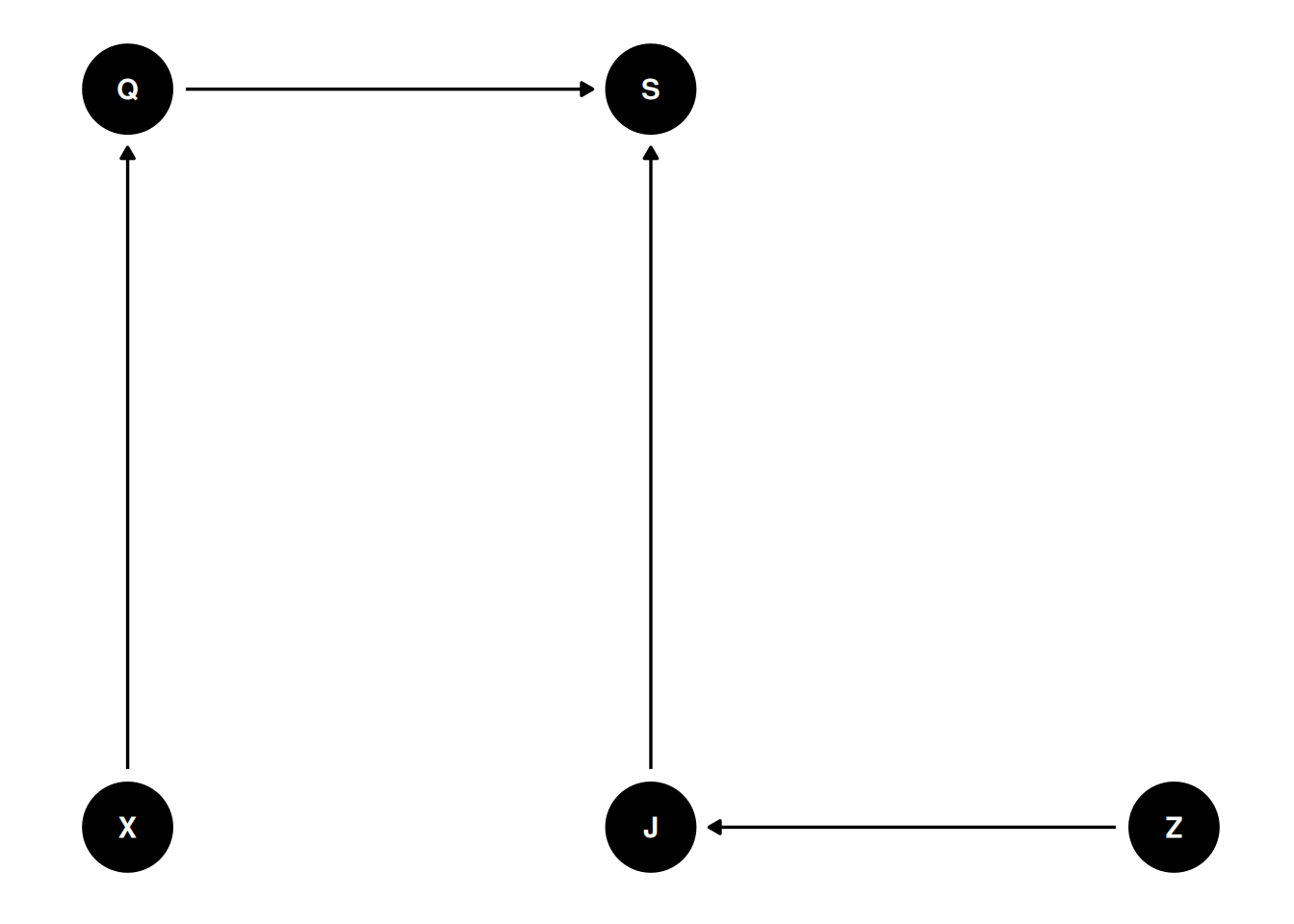
Lecture 08 Notes
Markov chain Monte Carlo
- Chain: sequence of draws from distribution
- Markov chain: history doesn’t matter, just current location
- Monte Carlo: some numerical algorithm that uses random simulation
Use in Bayesian statistics: to draw samples from a distribution
Sample each parameter value in proportion to its probability
There can be any number of dimensions (parameters)
At every step, the comparison is between the current combination of parameter values, and the candidate combination of parameter values. In this way, we don’t need to evaluate the entire grid
Algorithms
Metropolis algorithm
Simple version of Markov chain Monte Carlo (MCMC)
- simple, easy to code
- very general
- inefficient, especially at higher dimensions
- tuning step size where large often rejected or small where sampling is slow and samples are similar
Hamiltonian Monte Carlo
- physics simulation of gradients (local curvature of the distribution)
- friction-less particle moves in a random direction along gradient of probability distribution
- tuning step size where large often results in U-turns or small where sampling is slow
- particularly useful when probability distributions are more complex
- automatic differentiation translates model code into symbolic derivatives
Stan
Modern, open source, high-performance statistical computation tool.
data {
// the observed variables
vector[50] D;
vector[50] A;
vector[50] M;
}
parameters {
// the unobserved variables
real a;
real bM;
real bA;
real<lower=0> sigma;
}
model {
// compute the log posterior probability
vector[50] mu;
sigma ~ exponential( 1 );
bA ~ normal( 0 , 0.5 );
bM ~ normal( 0 , 0.5 );
a ~ normal( 0 , 0.2 );
for ( i in 1:50 ) {
mu[i] = a + bM * M[i] + bA * A[i];
}
D ~ normal( mu , sigma );
}- data
- represents the observed variables
- requires setting the length of each variable
- parameters
- represents the unobserved variables
- requires setting the types and constraints
- model
- represents the distributional parts of the model sufficient to compute the posterior probability
Diagnostics
- Trace plots
- graphical display of sequential samples plotted as a timeline
- optionally also include the warm up region
- “healthy” is stationary, remaining in the same general region through time (“hairy caterpillar”)
- Trace rank plots
- multiple chains are used to measure convergence where every chain explores the same distribution
- because of overlap between chains, trace rank plots can be easier to visualize multiple chains
- shows rank order
- “healthy” is switching between orders, no chain occupies consistently higher rank
- R-hat convergence measure
- R-hat is a ratio of variances, as total variance shrinks to average variance within chains, R-hat approaches 1
- no threshold, not a test, just a diagnostic criterion
- Number of effective samples
- number of effective samples
- “how long would the chain be if each sample was independent of the one before it?”
- when samples are auto correlated, there are fewer effective samples
- ineffective samples means that sequential samples share information
- Divergent transitions
- a kind of rejected proposal
- simulation diverges from true path
“When you have computation problems, often there’s a problem with your model” - Andrew Gelman
By problems with the models, he is referring to the probability assumptions, the priors, the statistical assumptions
Example: Judgement at Princeton
This is an example of modeling latent variables and item response models.
Scientific model
Wine quality (Q) is a latent variable meaning it is unobserved. There is no way to directly measure the quality of a wine because that is determined by preferences, etc.
We can observe the score (S) given by judges, who each have their own unobservable characteristics such as dispositions, opinions, biases, etc. Wine origin may affect the wine quality and the score (which may occur if judges’ origin biases them to wine origin).
If the blinding is not 100% accurate, if judges can guess the origin of the wine, they may be biased.
Estimand
What is the association between wine quality and wine origin, stratified by judge to improve precision of influence of wine origin?
Statistical model
In the lectures, Richard builds up the model in components, slowly adding complexity.
Association of wine score and quality
First, model the association of wine score with wine quality.
Wine quality is an unobserved parameter in the model. Since score is standardized, the average wine score will have an average quality.
\[S_{i} \sim Normal(\mu_{i}, \sigma)\] \[\mu_{i} = Q_{W[i]}\] \[Q_{j} \sim Normal(0, 1)\] \[\sigma \sim Exponential(1)\]
data(Wines2012)
d <- Wines2012
dat <- list(
S = standardize(d$score),
J = as.numeric(d$judge),
W = as.numeric(d$wine),
X = ifelse(d$wine.amer == 1, 1, 2),
Z = ifelse(d$judge.amer == 1, 1, 2)
)
mQ <- ulam(
alist(S ~ dnorm(mu, sigma),
mu <- Q[W],
Q[W] ~ dnorm(0, 1),
sigma ~ dexp(1)),
data = dat,
chains = 4,
cores = 4
)
Note: there is variability in the estimate unobserved parameter Q across wines.
Wine origin
Next, add the wine origin variable and stratify by it.
\[S_{i} \sim Normal(\mu_{i}, \sigma)\] \[\mu_{i} = Q_{W[i]} + O_{X[i]}\] \[Q_{j} \sim Normal(0, 1)\] \[O_{j} \sim Normal(0, 1)\]
\[\sigma \sim Exponential(1)\]
Judge effects
Lastly, introduce judge effects.
Judges’ biases are a competing cause and we use two additional latent variables (H and D) to measure them. \(\mu_{i}\) is the expected score of a wine and it is calculated by multiplying the judge discrimination (D) by wine quality added to origin (O) subtracted by judge harshness (H). Harshness represents how good a wine has to be to give it an average score. Discriminatory judges give very disperse scores to different wines, whereas non-discriminatory judges give similar scores to all wines. This formulation comes from common judge or item response models.
\[S_{i} \sim Normal(\mu_{i}, \sigma)\] \[\mu_{i} = (Q_{W[i]} + O_{X[i]} - H_{J[i]})D_{J[i]}\] \[Q_{j} \sim Normal(0, 1)\] \[O_{j} \sim Normal(0, 1)\] \[H_{j} \sim Normal(0, 1)\] \[D_{j} \sim Normal(0, 1)\] \[\sigma \sim Exponential(1)\]
We see a lot of variation between judges. Judge 4 has a high harshness value compared to judges 5 and 6. Including judge specific latent effects helps us provide better estimates by dealing with these known contributing causes of wine score.