One prior distribution for each cluster
\([\alpha_{j}, \beta_{j}] \sim MVNormal([\bar{\alpha}, \bar{\beta}], R, [\sigma, \tau])\)
\(R \sim LKJCorr(4)\)
The LKJ prior is a prior distribution for correlations.
See here for plotting LKJCorr distributions.
Outcome: contraceptive use
Variables: age, living children, urban/rural, districts
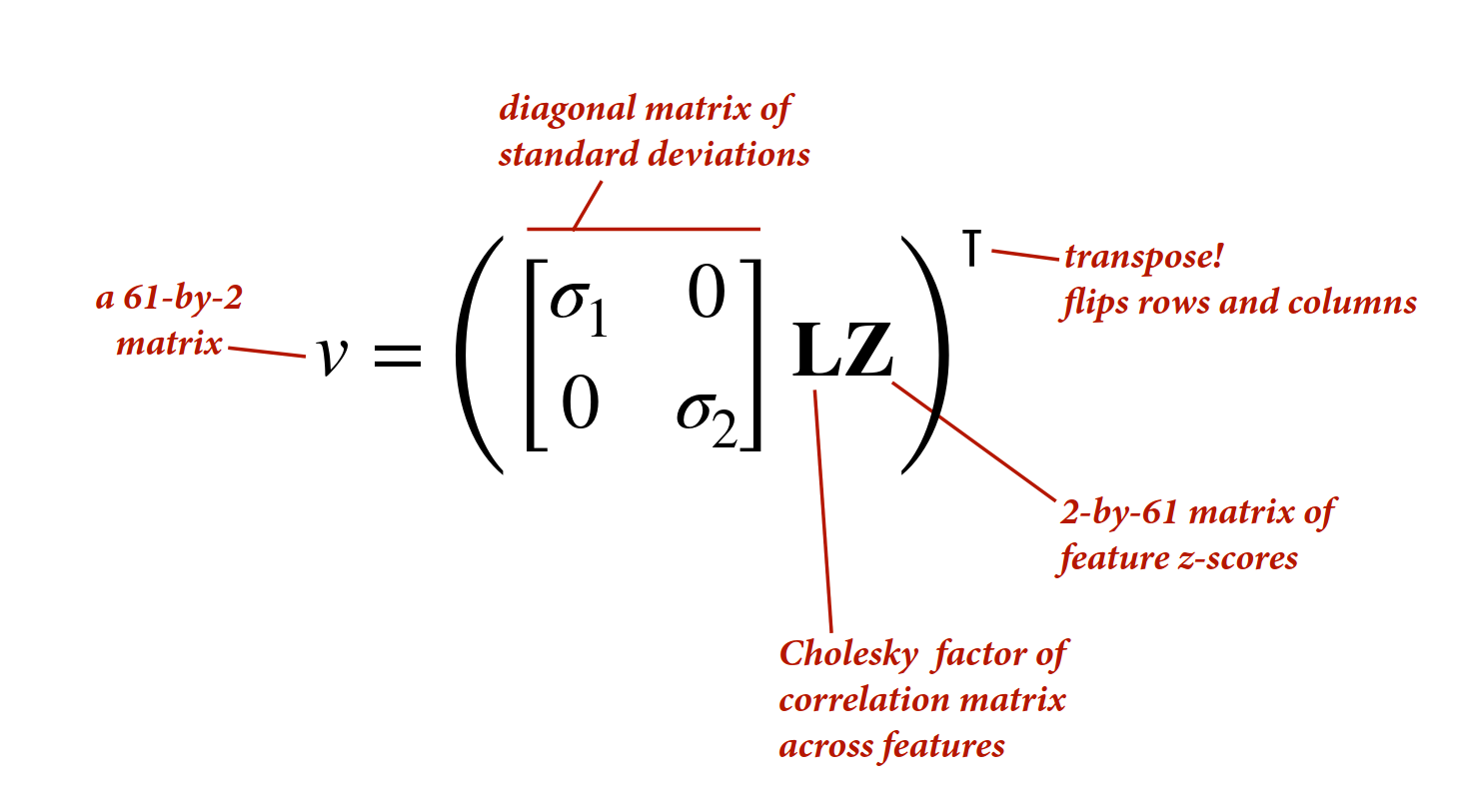
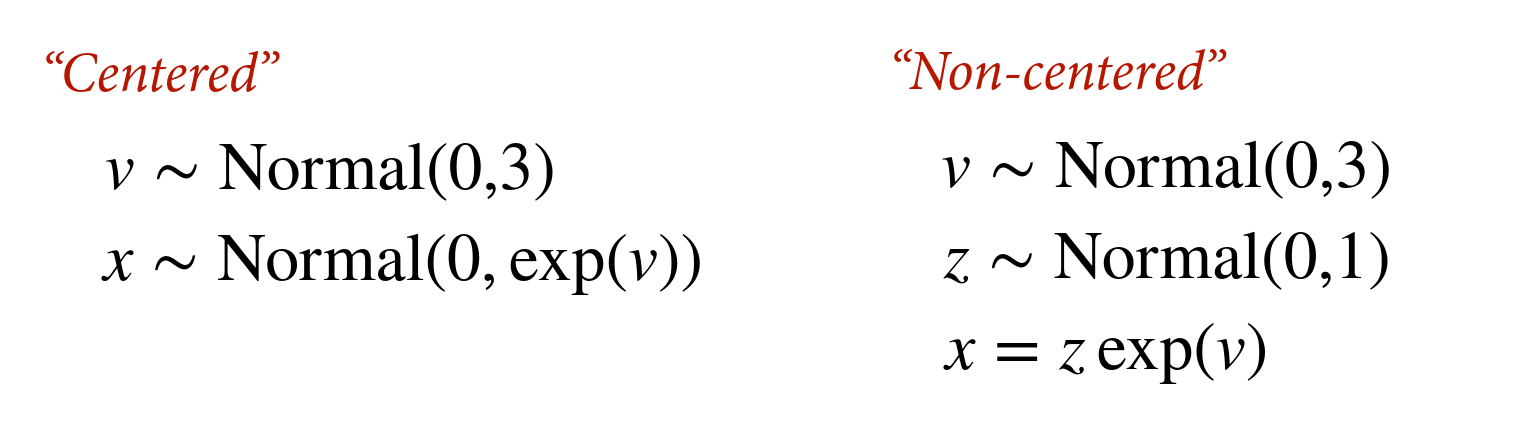coords <- data.frame(
name = c('A', 'C', 'D', 'K', 'U'),
x = c(1, 2, 3, 1.5, 2.5),
y = c(0, 0.5, 0, -1, -1)
)
dagify(
C ~ A + K + D + U,
K ~ A + U,
U ~ D,
coords = coords
) |> ggdag(seed = 2, layout = 'auto') + theme_dag()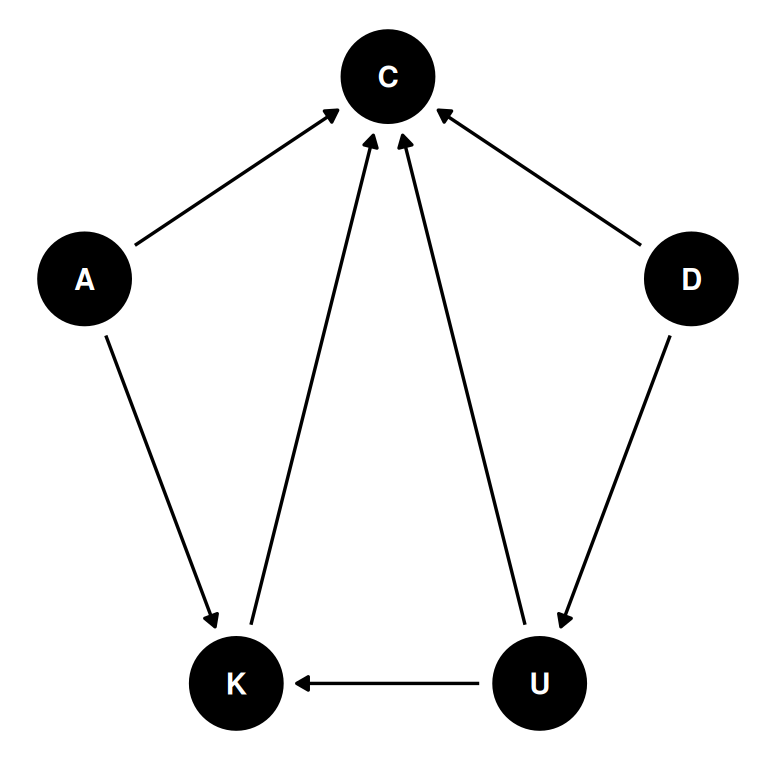
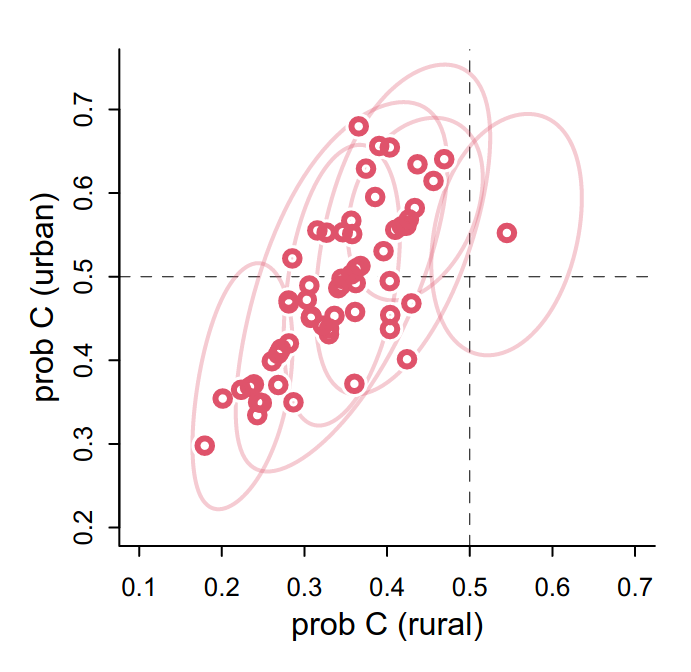From the previous lecture, the varying intercepts for district and slopes for urban.
\(C_{i} \sim Bernoulli(D_{i}, p_{i})\)
\(logit(p_{i}) = \alpha_{D[i]} + \beta_{D[i]}U_{i}\)
\(\alpha_{j} = \bar{\alpha} + Z_{\alpha, j} * \sigma\)
\(\beta_{j} = \bar{\beta} + Z_{\beta, j} * \sigma\)
\(Z_{\alpha, j} \sim Normal(0, 1)\)
\(Z_{\beta, j} \sim Normal(0, 1)\)
\(\bar{\alpha}, \bar{\beta} \sim Normal(0, 1)\)
\(\sigma, \tau \sim Exponential(1)\)
There is useful information to transfer across features, here we note there is a correlation between rural and urban probability of use within districts. A model that uses two 1-dimensional distributions (intercepts and slopes) does not consider the covariance structure between rural and urban within district.
Comparing the centered and non-centered model specification for the model using the multivariate normal specification with correlated features.
Simulating a synthetic dataset for this kind of complex system is challenging and is likely best done with more detailed tools than eg. expecting a linear responses, instead with eg. an agent based model.
Because of high curvature, the physics simulation runs off the surface. One option is to choose a smaller step size, but this results in much longer sampling time. Alternatively, re-express the “centered” model as a “non-centered” model.
