p <- seq(0, 1, 0.01)
ggplot(data.table(logit_p= logit(p), p = p)) + geom_line(aes(logit_p, p))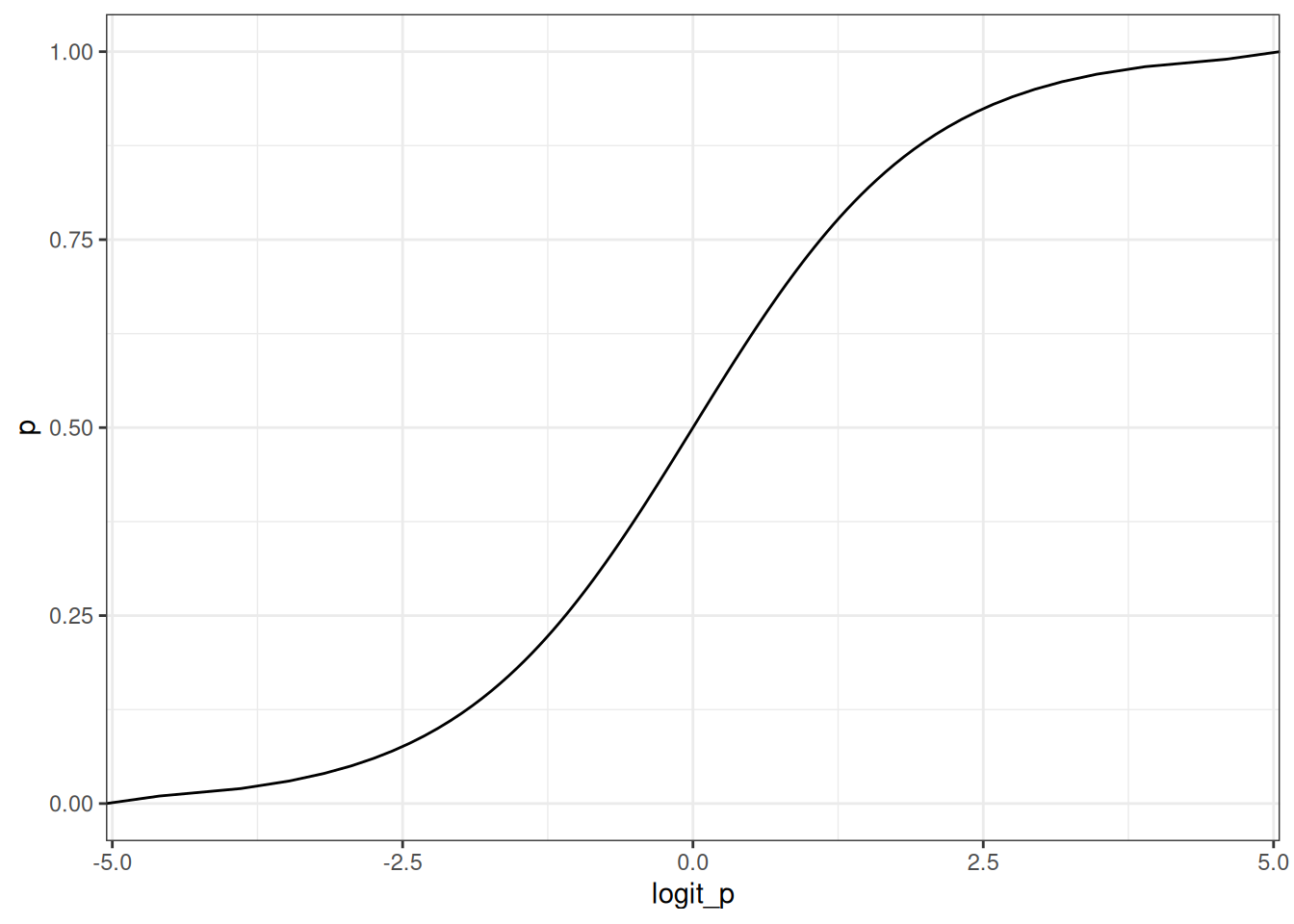
Lecture 09 Notes
Generalized linear models
Modeling events
Like tide prediction engines (analog computers), the gears inside the machine bear no resemble to the observable predictions that they put out.
- Events are discrete, unordered outcomes
- Observations are counts of events
- Unknowns estimated are on the probability or log-odds/logit scale (probability it happens / probability it does not happen)
Linear models: expected value is an additive linear combination of parameters. Can only do this with the normal distribution because it is unbounded.
Other events are bounded. For example, probability of events are restricted to 0-1.
Generalized linear models: expected value is some function of an additive combination of parameters.
\(Y_{i} \sim Bernoulli(p_{i})\)
\(f(p_{i}) = \alpha + \beta_{{X}} X_{i} + \beta_{Z} Z_{i}\)
- \(Y_{i}\): 0/1 outcome
- \(p_{i}\): probability of event
- \(f(p_{i})\): f() maps probability scale to linear model scale
- \(\alpha + \beta_{{X}} X_{i} + \beta_{Z} Z_{i})\): can be any real value
\(f\) is the link function
\(f(p_{i} = \alpha + \beta_{{X}} X_{i} + \beta_{Z} Z_{i})\)
\(f^{-1}\) is the inverse link function.
\(p_{i} = f^{-1}(\alpha + \beta_{{X}} X_{i} + \beta_{Z} Z_{i})\)
Logistic regression: binary [0,1] outcome and logit link, with Bernoulli distribution
Binomial regression: count [0, N] outcome and logit link, with Binomial distribution (Binomimal variables are sums of Bernoulli variables)
Distributions
The distribution is matched to constraints on observed variables and the link function is matched to this distribution.
- Exponential distribution: time to event that has a constant rate. Greater than 0, single parameter \(\lambda\) that defines the rate.
- Binomial distribution: count events bounded in an observation window. Some number of trials
- Poisson distribution: count events with constant rate. This is the count distribution of the exponentially distributed events. We don’t know the maximum or number of coin tosses.
- Gamma distribution: sum up exponential processes.
- Normal distribution: Gamma distribution with large mean converges to the Normal distribution.
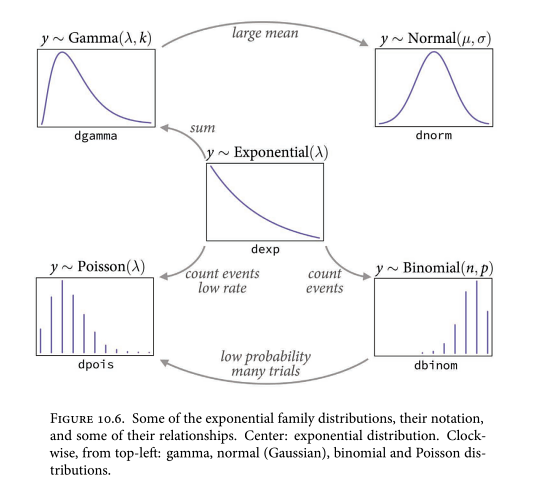
Distribution you want to use to model an observed variable is governed by the constraints on observation. Eg. you can’t have negative counts. You can’t use some test to decide if your data are “Normal”.
Logit link
Bernoulli and binomial models most often use the logit link.
\(logit\) is the link function
\(logit(p_{i} = \alpha + \beta_{{X}} X_{i} + \beta_{Z} Z_{i})\)
\(logit^{-1}\) (logistic) is the inverse link function.
\(p_{i} = logit^{-1}(\alpha + \beta_{{X}} X_{i} + \beta_{Z} Z_{i})\)
Logit link is a harsh transformation
Logistic priors
The logit link compresses parameter distributions. Anything above +4 = almost always, anything below -4 = almost never.
Example: UC Berkeley Admissions
- Graduate school applications for 1973 UC Berkeley
- Stratified by department and gender of application
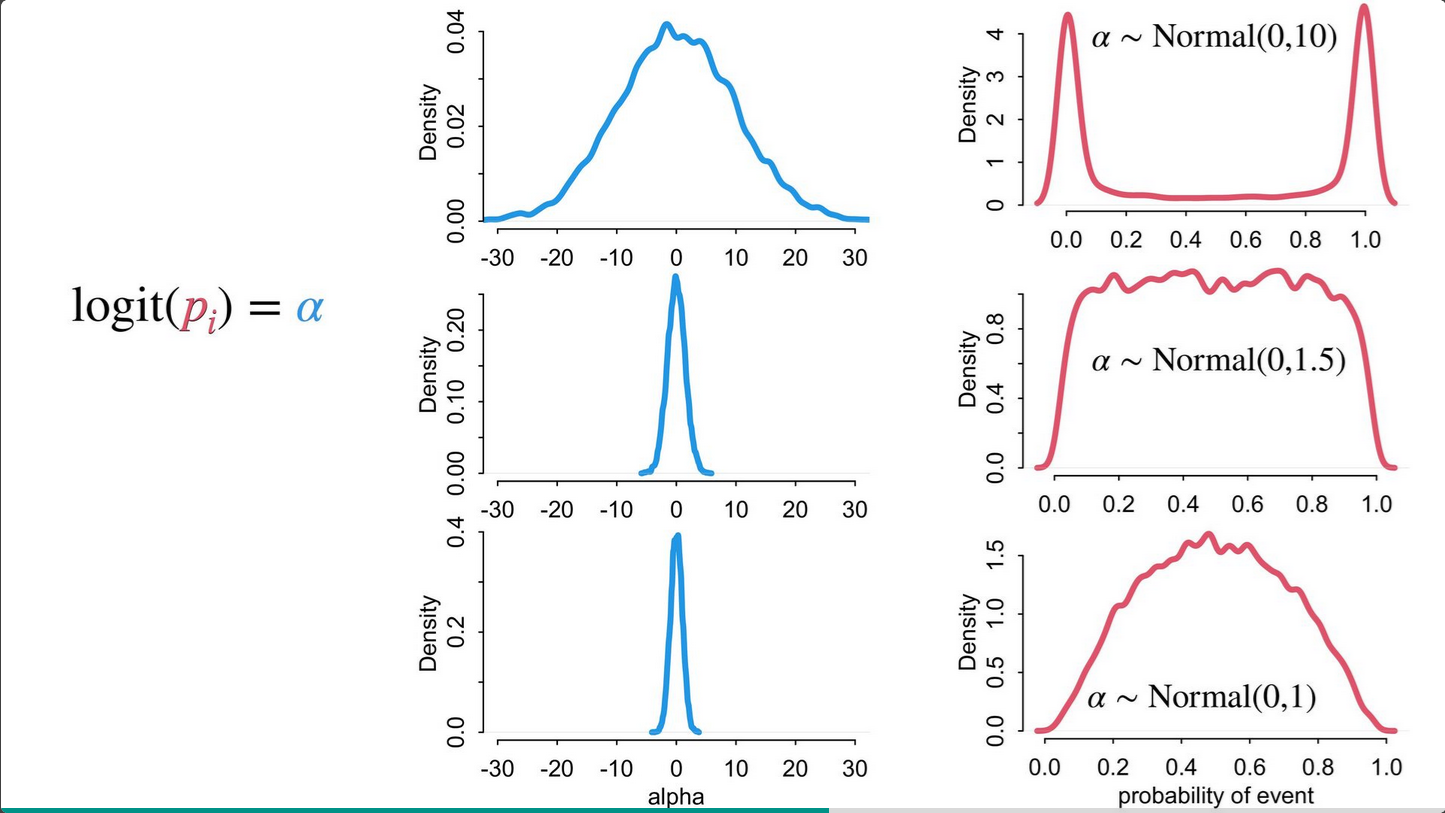
See more here:
Traag, V.A. and Waltman, L., 2022. Causal foundations of bias, disparity and fairness. arXiv preprint arXiv:2207.13665.
1. Estimand
suppressPackageStartupMessages(library(ggdag))
coords <- data.frame(
name = c('G', 'D', 'A', 'G_star', 'R', 'U'),
x = c(1, 2, 3, 2, 4, 4),
y = c(0, 1, 0, -1, -1, 1)
)Was there gender discrimination in graduate admissions?
- G: gender
- A: admission
- D: department
Typically, department is considered a mediating variable
What can the “causal effect of gender” mean?
dagify(
A ~ R + G_star + D,
G_star ~ G,
D ~ G,
coords = coords
) |> ggdag(seed = 2, layout = 'auto') + theme_dag()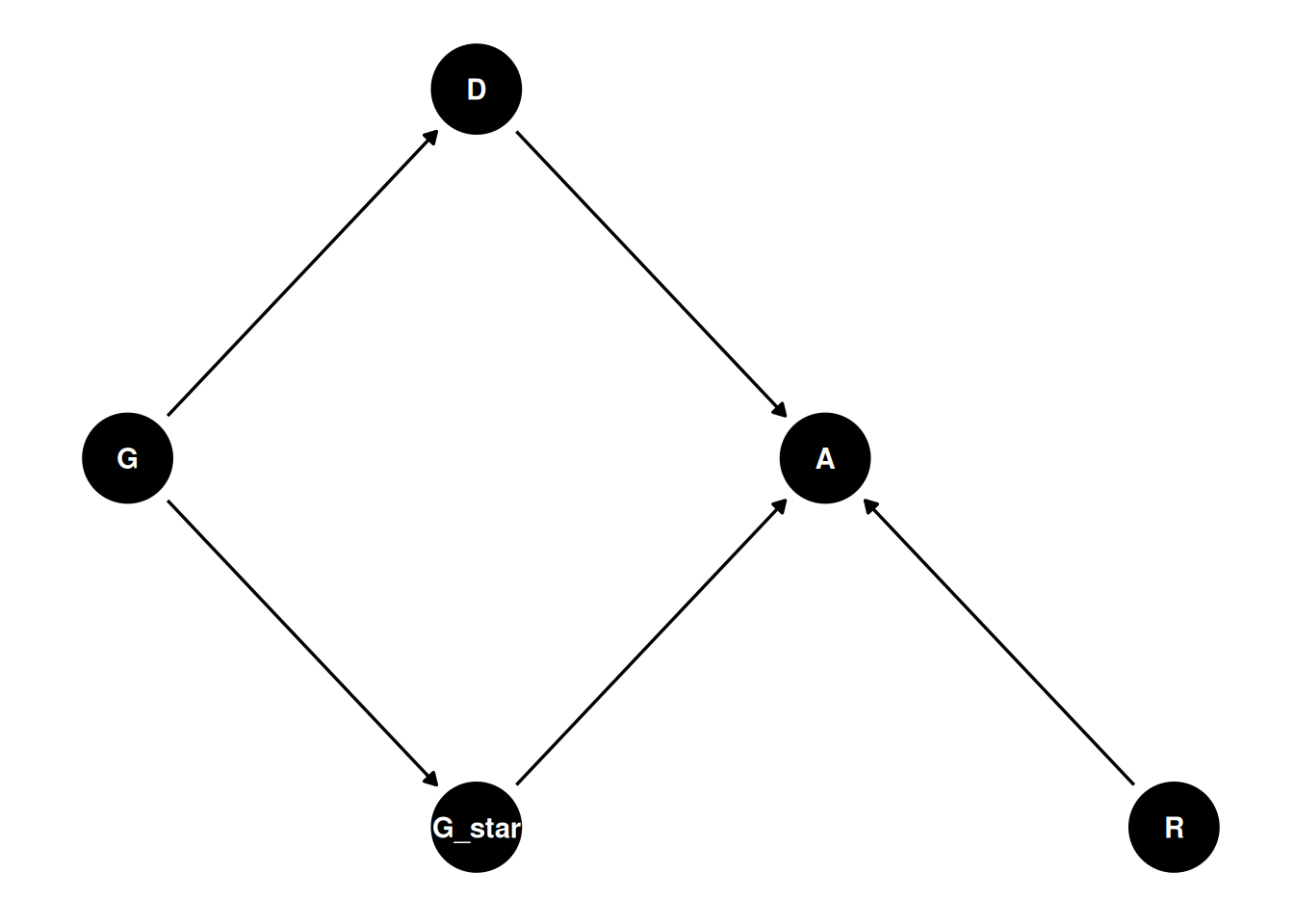
Which path represents “discrimination”?
- direct discrimination: status-based discrimination from G -> A
- structural discrimination: indirect through department G -> D -> A
- total discrimination: G -> A and G -> D -> A, what individuals experience
For now, we will ignore the unobserved confounds between the mediator and the outcome.
2. Generative model
- Set number of applicants
- Sample gender
- Sampled with preference for different departments by gender (indirect effect)
- Define acceptance rate for departments
- Simulate acceptance
Changing the acceptance rate where acceptance differs by department and gender, pattern of differences in acceptance rates is the same in this simulated data. This illustrates the fundamental problem of determining if discrimination is occuring.
Generative model could be greatly improved:
- Admission rates depend upon size of applicant pool and the distribution of qualifications
- Admission rates are then based on ranking applicants to a set number of spaces
3. Statistical models
Total causal effect of G
\(A_{i} \sim Bernoulli(p_{i})\)
\(logit(p_{i}) = \alpha[G_{i}]\)
\(\alpha = [\alpha_{1}, \alpha_{2}]\)
Direct causal effect of G
\(A_{i} \sim Bernoulli(p_{i})\)
\(logit(p_{i}) = \alpha[G_{i}, D_{i}]\)
\(\alpha = \begin{bmatrix} \alpha_{1, 1} & \alpha_{1, 2} \\ \alpha_{2, 1} & \alpha_{2, 2}\end{bmatrix}\)
4. Validate the model
Use inverse logit function to transform variables back on probability scale. Determine if known parameters are recovered by the model.
5. Analyze the data
To use a binomial distribution, aggregate the long format data into acceptance sums for each gender and department. This is equivalent to using the original data with a Bernoulli distribution.
- inspect trace plots and trank plots to ensure chains are well mixed
- extract samples from the posterior
- convert the entire posterior distribution back to the prediction scale with the inverse logit
- compute contrasts for total effect (across genders) and direct effects (within departments)
Post stratification
Back to the question: what’s the average direct effect of gender across departments?
This depends on the perception of gender on the admission officer
dagify(
A ~ G_star + D,
G_star ~ G,
D ~ G,
coords = coords
) |> ggdag(seed = 2, layout = 'auto') + theme_dag()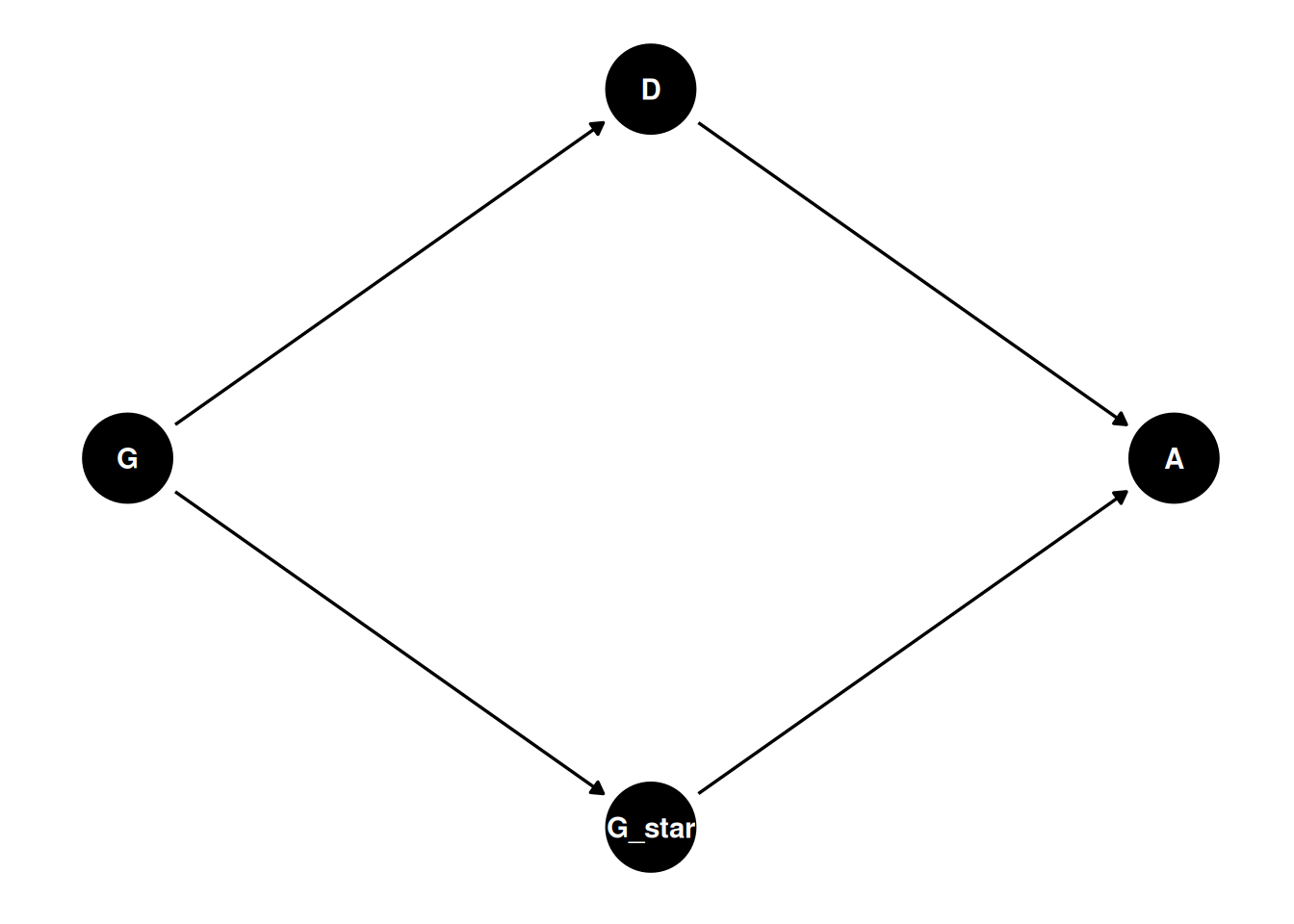
To calculate the causal effect of G*, we must average (marginalize) over the departments. (Note still assuming no confounds).
Simulate as if all applicants are women, then simulate as if all applicants are men. Then compute the contrasts.
Post stratification is reweighing estimates for target population. Eg. at a different university, the distributions would differ, and we could predict how the consequences of intervention differ
Survival analysis
How long did an event take to happen? Time-to-event.
Cannot ignore censored cases, where event never happened.
- Left-censored: don’t know when time started
- Right-censored: observation ended before event
Example: cat adoptions
Adoption rates of black and non-black cats
Events: adopted, or something else (death, escape, censored)
Outcome variables: days to event. Appropriate distributions are exponential and gamma. Exponential arises from a single part that needs to fail before the so-called machine dies, whereas the Gamma distribution requires multiple parts to fail.
For simplest situation, time to adoption, this represents it:
\(D_{i} \sim Exponential(\lambda_{i})\)
\(p(D_{i} | \lambda_{i}) = \lambda_{i} exp(-\lambda_{i} D_{i})\)
But what about the censored cats?
Event happened = cumulative distribution, probability of event happening up to time x
Event didn’t happen = complementary cumulative distribution, probability event hasn’t occurred up to time x
\(D_{i} = 1 \sim Exponential(\lambda_{i})\)
\(D_{i} = 0 \sim Exponential-CCDF(\lambda_{i})\) (not-yet-adoptions)
\(\lambda_{i} = 1 / \mu_{i}\)
\(log \mu_{i} = \alpha_{CID[i]}\)
- \(D_{i} = 1\): observed adoptions
- \(D_{i} = 0\): not yet adoptions